Counting Votes

Counting votes is an important part, perhaps the most important part, of any electoral system. Here, we explain it for Local Proportional Representation in three increasing levels of detail.

The overall goal of the count is to identify the best set of candidates for the region with the constraint that exactly one of them is in each riding.

In the following there are two important things to remember:

1. candidates are ranked on the ballot – 1st choice, 2nd choice, etc.
2. quota defines the number of votes required to win a seat; call that number Q.

Detailed examples can be seen in the modelling details; scroll down to choose a region and then click the “See how the votes transferred” link.

Counting Votes: The High-Level View

The counting process under Local PR is done in rounds where each round elects one candidate. It maximizes the value of every ballot while keeping every candidate in the running as long as possible.

In each round, a riding is won by the first candidate to acquire the number of votes needed to win a seat. This is called reaching quota. If no candidate in the region reaches quota based on first ranked preferences (the “1”s), the ballots of the candidate with the fewest votes are redistributed to candidates who are next-ranked on these ballots. This is repeated until one of the remaining candidates reaches quota. Once a candidate reaches quota, he or she is elected and other candidates from the same riding are eliminated, concluding the round.

Subsequent rounds are started with all of the original candidates except those who have been eliminated from ridings with an elected candidate. Ballots for the eliminated candidates are redistributed to next-ranked candidates. The round continues until another candidate¹ reaches quota. Rounds continue until one locally-nominated candidate has been elected in each riding.

Counting Votes: The Detailed View

At any given time each candidate is in one of four possible states:

• Elected: candidates that have reached quota and are declared winners
• Hopeful: candidates that could still be elected
• Suspended: candidates whose votes are redistributed during one of the rounds
• Not Elected: candidates that have been eliminated from the race

All of the candidates start out as Hopeful.

We’ll trace what happens to one particular ballot during the counting process in an imaginary election.

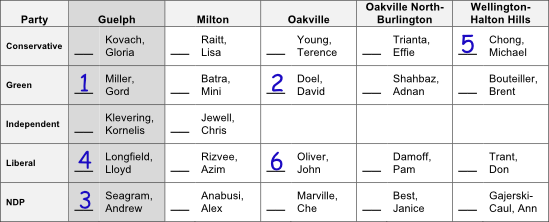
Imagine one pile for each candidate’s ballots. Our ballot goes on Gord Miller’s pile because Miller was ranked number 1.

Suppose that Miller is the candidate with the fewest ballots on his pile.
That signals that he is the next person to be Suspended; that is, his state changes from Hopeful to Suspended. This ballot will then be placed on the pile of the next highest ranked Hopeful candidate, David Doel.

At some point Doel becomes the candidate with the smallest pile of ballots and is also Suspended. This ballot then goes to Andrew Seagram’s pile. Likewise, Seagram is eventually Suspended and the ballot goes to Lloyd Longfield.

Imagine that Longfield is popular and there are now 50,000 ballots on his pile but he only needs 40,000 votes to win. That number, 40,000, is called the quota. Quota is the equivalent of 50% + 1 in a FPTP election, the minimum number of votes to guarantee victory (although it could be less with vote splitting). Longfield is now declared Elected.¹

Unfortunately for the remaining Hopeful candidates in Longfield’s riding, they can’t be elected without breaking the rule about electing exactly one MP in each riding. They are therefore declared Not Elected.

This concludes the first round. All candidates with a state of Elected, Hopeful or Suspended are now returned to the Hopeful state. The other candidates in Longfield’s riding that were declared Not Elected remain that way. Ballots are once again put on the piles of the first preference candidate. If that candidate is Not Elected, the ballot is transferred to the next preference that is still Hopeful.

Counting is now restarted from the beginning and runs until a new candidate reaches quota and is declared Elected. As before, if no candidate has reached quota, the candidate with the fewest votes is Suspended and their ballots redistributed. Longfield will once again reach quota and be declared Elected. His surplus votes (he got 50,000 with transfers but only needs 40,000 to win) will be fairly distributed. In this example, the ballot is transferred to Michael Chong. But ⁴⁄₅ of this ballot (40,000/50,000) was needed to elect Longfield, so Chong only gets the remaining ¹⁄₅.

The round ends when a new candidate reaches quota and is declared Elected and other candidates in his or her riding are Not Elected. The remaining Elected, Suspended, and Hopeful candidates are again restored to the Hopeful state and the next round begins. This continues until every riding has an elected candidate.

Counting Votes: The Algorithm

For those who prefer to be yet more rigorous in describing the procedure, we can express it as pseudocode for a computer algorithm:

for each candidate, c:
  c.state = Hopeful

while (some seats remain unfilled):
  newlyElected = doOneRound
  for each candidate, c:
    if (c and newlyElected are in the same riding):
      c.state = NotElected
    else
      c.state = Hopeful

where doOneRound is defined as:

while (true):
  w = the hopeful candidate having the most votes
  if (w reached quota)
    if (w.state == Elected):
      fairly transfer surplus to hopeful candidates
    else:
      w.state = Elected
      return w

  else if (only 1 hopeful candidate remains, h):
    # Due to exhausted ballots, it's possible for a candidate to be 
    # elected without reaching quota
    h.state = Elected
    return h

  else:
    s = the hopeful candidate having the fewest votes
    s.state = suspended
    fairly transfer votes from s to hopeful candidates